Controlling Pressure
Overview
Teaching: 10 min
Exercises: 0 minQuestions
Why do we want to control the pressure of our MD-simulations?
What pressure control algorithms are commonly used?
What are the strengths and weaknesses of these common barostats?
Objectives
Introduction
The role of pressure control algorithms is to keep pressure in the simulation system constant or to apply an external stress to the simulated system.
How is pressure kept constant in a simulation? Pressure is kept on its target value by adjusting the volume of a periodic simulation system. What defines pressure is a simulation system, how can we measure pressure in a simulation? From the physical point of view pressure is a force exerted by collision of particles with the walls of a closed container. The virial equation is commonly used to obtain the pressure from a molecular dynamics simulation. According to this equation pressure in a simulation has two components:
- Pressure is kept on its target value by adjusting the volume of a periodic simulation system.
- Pressure is a force exerted by collision of particles with the walls of a closed container.
- The virial equation is used to obtain the pressure:
$ \qquad {P}=\frac{NK_{B}T}{V}+\frac{1}{3V}\langle\sum{r_{ij}F_{ij}}\rangle$
The first term in this equation describes pressure of an ideal gas (meaning no interaction between molecules). The second contribution comes from internal forces acting on each atom. The virial equation is well suited for MD since forces are evaluated at each simulation step anyway, and they are readily available.
- The first term in this equation describes pressure of an ideal gas (no interaction between molecules).
- The second contribution comes from internal forces acting on each atom.
- Well suited for MD because forces are evaluated at each simulation step.
As with temperature control, there are different algorithms of pressure control for MD simulation.
Pressure Control Algorithms
Barostats regulate pressure by adjusting the volume of the simulated system. In practice this done by scaling coordinates of each atom is a system by a small factor, so that the size of the system changes. The methods of maintaining pressure fall into categories similar to categories of temperature regulation.
- Regulate pressure by adjusting the volume
- In practice barostats do that by scaling coordinates of each atom by a small factor.
- The methods of maintaining temperature fall into four categories:
- Weak coupling methods
- Extended system methods
- Stochastic methods
- Monte-Carlo methods
1. Weak coupling methods
Berendsen pressure bath coupling.
Berendsen barostat is conceptually similar to Berendsen thermostat. This thermostat is available in all simulation packages. To regulate pressure this algorithm changes the volume by an increment proportional to the difference between the internal pressure and pressure in a weakly coupled bath. Berendsen thermostat is very efficient in equilibrating the system. However, it does not sample the exact NPT statistical ensemble. Often pressure fluctuations with this barostat are smaller then they should be. It is also known that this algorithm induces artifacts into simulations of inhomogeneous systems such as aqueous biopolymers or liquid/liquid interfaces.
- Conceptually similar to Berendsen thermostat.
- Available in all simulation packages.
- Change the volume by an increment proportional to the difference between the internal pressure and pressure in a weakly coupled bath.
- Very efficient in equilibrating the system.
Downsides:
- Does not sample the exact NPT statistical ensemble.
- Induces artifacts into simulations of inhomogeneous systems such as aqueous biopolymers or liquid/liquid interfaces.
- Should be avoided for production MD simulations.
The time constant for pressure bath coupling is the main parameter of the Berendsen thermostat. The pressure of the system is corrected such that the deviation exponentially decays with a lifetime defined by this constant.
Reference: Molecular dynamics with coupling to an external bath
2. Extended system methods
In the classical work Andersen proposed a pressure control method with an extended system variable. It is based on including an additional degree of freedom corresponding to the volume of a simulation cell which adjusts itself to equalize the internal and external pressure. In this method an additional degree of freedom serves as a piston, and is given a fictitious “mass”. The choice of piston “mass” determines the decay time of the volume fluctuations. The Parrinello-Rahman barostat, the Nosé-Hoover barostat, and the Martyna-Tuckerman-Tobias-Klein (MTTK) are all based on the Andersen barostat.
- Extended system methods originate from the classical theoretical work of Andersen.
- He included an additional degree of freedom, the volume of a simulation cell.
- Volume adjusts itself to equalize the internal and external pressure.
- Volume serves as a piston, and is given a fictitious “mass” controlling the decay time of pressure fluctuations.
- Extended system methods are time-reversible. They can be used to integrate backwards, for example, for transition path sampling.
Parrinello-Rahman barostat
The Andersen method was extended by Parrinello and Rahman to allow changes in the shape of the simulation cell, and later it was further extended by the same authors to include external stresses Parrinello and Rahman. This method allows additionally for a dynamic shape change and is useful to study structural transformations in solids under external stress. Equations of motion are similar to Nosé-Hoover barostat, and in most cases you would combine the Parrinello-Rahman barostat with the Nosé-Hoover thermostat.
- Extension of the Andersen method allowing changes in the shape of the simulation cell.
- Further extended to include external stresses.
- Useful to study structural transformations in solids under external stress.
- Equations of motion are similar to Nosé-Hoover barostat, and in most cases it is used with the Nosé-Hoover thermostat.
The drawback is that decay of the volume fluctuations may oscillate with the frequency proportional to the piston mass.
Downsides:
- Volume may oscillate with the frequency proportional to the piston mass.
Nosé-Hoover barostat
Nosé and Klein were the first to apply method analogous to Andersen’s barostat for molecular simulation. This variation was further improved by Hoover. It is widely used now under the name “Nosé-Hoover barostat” Constant pressure molecular dynamics algorithms.
- First application of the method analogous to Andersen’s barostat for molecular simulation.
- The Nosé-Hoover equations of motion are only correct in the limit of large systems.
MTTK (Martyna-Tuckerman-Tobias-Klein) barostat.
Nosé-Hoover method was not free of issues. It was observed that the Nosé-Hoover equations of motion are only correct in the limit of large systems. To solve this problem Martyna-Tuckerman-Tobias-Klein (1996) introduced their own equations of motion. The MTTK method is a natural extension of the Nosé-Hoover and Nosé-Hoover chain thermostat, and in most cases you would combine the MTTK barostat with the Nosé-Hoover thermostat. The nice feature of this thermostat is that it is time-reversible. This means that it can be used to integrate backwards as needed, for example, for transition path sampling.
- Extension of the Nosé-Hoover and Nosé-Hoover chain thermostat, performs better for small systems.
3. Stochastic methods
Langevin piston pressure control.
Langevin piston barostat is based on Langevin thermostat. The equations of motion resemble MTTK equations, but an additional damping (friction) force and stochastic force are introduced. A suitable choice of collision frequency then eliminates the unphysical oscillation of the volume associated with the piston mass. In this way it is similar to the weak coupling Berendsen algorithm, but in contrast it yields the correct ensemble.
- Based on Langevin thermostat.
- The equations of motion resemble MTTK equations.
- An additional damping (friction) force and stochastic force are introduced.
- Random collisions eliminate oscillation of the volume associated with the piston mass.
Reference: Constant pressure molecular dynamics simulation: The Langevin piston method
| MTTK and Langevin barostats produce identical ensembles | Langevin barostat oscillates less then MTTK and converges faster due to stochastic collisions and damping. |
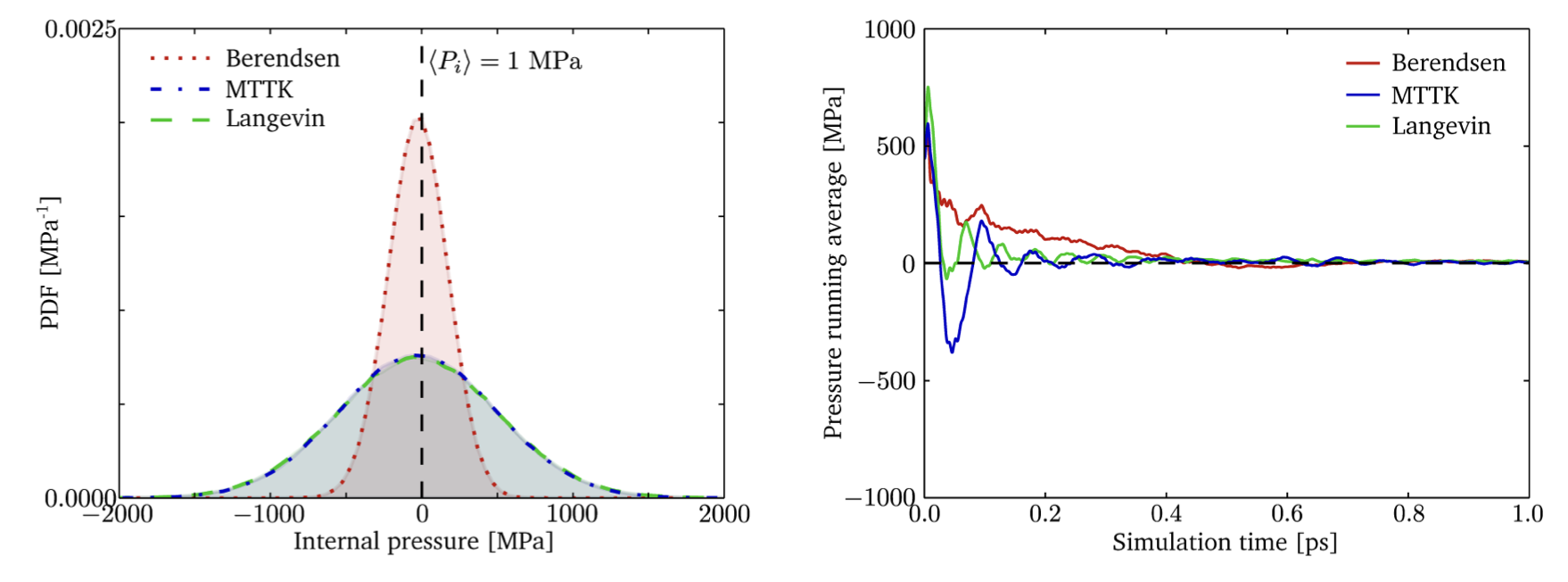
MTTK and Langevin produce identical ensembles, but Langevin barostat oscillates less then MTTK and converges faster due to stochastic collisions and damping.
Reprinted with permission from Rogge et al. 2015, A Comparison of Barostats for the Mechanical Characterization of Metal−Organic Frameworks, J Chem Theory Comput. 2015;11: 5583-97. doi:10.1021/acs.jctc.5b00748. Copyright 2015 American Chemical Society.
Stochastic Cell Rescaling
The stochastic cell rescaling algorithm was developed by Bernetti and Bussi (2020) as an improved version of the Berendsen pressure bath that samples correct volume fluctuations. It adds a stochastic term to the calculation of the rescaling matrix that causes the local pressure fluctuations to be correct for the canonical (NPT) statistical ensemble while retaining the fast first order decay of the pressure deviations from the target pressure.
- Improved version of the Berendsen barostat.
- Adds stochastic term to rescaling matrix.
- Produces correct fluctuations of local pressure for NPT ensemble.
Therefore stochastic cell rescaling can be applied during both equilibration, while the pressure is still far from the target, which would lead to undesired oscillations when using extended system methods like Parrinello-Rahman or MTTK, as well as during production-md (data collection), where it is important to sample from a correct statistical ensemble.
- Pressure converges fast without oscillations.
- Can be used for all stages of MD, including production.
4. Monte-Carlo pressure control.
Recently several efficient Monte Carlo methods have been introduced. Monte Carlo pressure control samples volume fluctuations at a predefined number of steps at a given constant external pressure. It involves generation of a random volume change from a uniform distribution followed by evaluation of the potential energy of the trial system. The volume move is then accepted with the standard Monte-Carlo probability. Virial is not computed by Monte-Carlo methods, so pressure is not available at runtime, and it is also not printed in energy files.
- Recently several efficient Monte Carlo methods have been introduced.
- Sample volume fluctuations at a predefined number of steps at a given constant external pressure.
- Generate a random volume change, evaluate the potential energy. The volume move is then accepted with the standard Monte-Carlo probability.
- Do not compute virial, so pressure is not available at the runtime, and not printed in energy files.
References:
- Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm
- Constant pressure hybrid Molecular Dynamics–Monte Carlo simulations
Pitfalls
To ensure stability of a simulation volume must be adjusted very slowly with a small increments at each simulations step. Rapid change of the system size may lead to simulation crash. This can occur, for example when pressure coupling is turned on when you begin simulation from a cold start and turn pressure coupling too early in the heating process. In this case, the difference between the target and the real pressure will be large, the program will try to adjust the density too quickly, and bad things (such as SHAKE failures) are likely to happen.
- If the difference between the target and the real pressure is large, the program will try to adjust the density too quickly.
- Rapid change of the system size may lead to simulation crash.
- To ensure stability of a simulation volume must be adjusted very slowly with a small likely
Conclusion
Each barostat or thermostat technique has its own limitations and it is your responsibility to choose the most appropriate method or their combination for the problem of interest.
Selecting barostats in molecular dynamics packages
| Thermostat\MD package | GROMACS | NAMD | AMBER |
|---|---|---|---|
| Berendsen | pcoupl = Berendsen | BerendsenPressure on | barostat = 1 |
| Stoch. cell rescaling | pcoupl = C-rescale | ||
| Langevin | LangevinPiston on | ||
| Monte-Carlo | barostat = 2 | ||
| Parrinello-Rahman | pcoupl = Parrinello-Rahman | ||
| MTTK | pcoupl = MTTK |
Key Points