Periodic Boundary Conditions

Overview

Teaching: 20 min
Exercises: 0 min

Questions

• How to simulate a bulk (gas, liquid or solid) system by using only a small part?

Objectives

• Understand why and when periodic boundary conditions are used.

• Understand how shape and size of a periodic box can affect simulation.

• Learn how to set periodic box parameters in GROMACS and NAMD.

What is PBC and why is it important?

In most cases we want to simulate a system in realistic environment, such as solution. If one tries to simulate a protein in a droplet of water, it will simply evaporate.

The boundary to contain molecules in simulation is needed to preserve thermodynamic properties like temperature, pressure and density. The use of PBC in simulations allows the inclusion of bulk solvent or crystalline environments. In other words periodic boundary conditions make it possible to approximate an infinite system by using a small part (unit cell). A unit cell in MD is usually referred to as periodic box.

• In most cases we want to simulate a system in realistic environment, such as solution.
• Try simulating a droplet of water, it will simply evaporate.
• We need a boundary to contain water and control temperature, pressure, and density.
• Periodic boundary conditions allow to approximate an infinite system by using a small part (unit cell).

To implement PBC the unit cell is surrounded by translated copies in all directions to approximate an infinitely large system. When one molecule diffuses across the boundary of the simulation box it reappears on the opposite side. So each molecule always interacts with its neighbours even though they may be on opposite sides of the simulation box. This approach replaces the surface artifacts caused by the interaction of the isolated system with a vacuum with the PBC artifacts which are in general much less severe.

• Unit cell is surrounded by an infinite number of translated copies in all directions (images).
• When a particle in unit cell moves across the boundary it reappears on the opposite side.
• Each molecule always interacts with its neighbors even though they may be on opposite sides of the simulation box.
• Artifacts caused by the interaction of the isolated system with a vacuum are replaced with the PBC artifacts which are in general much less severe.

Choosing periodic box size and shape.

Box shape

Cubic periodic box

A cubic box is the most intuitive and common choice, but it is inefficient due to irrelevant water molecules in the corners. The extra water will make your simulation run slower.

• A cubic box is the most intuitive and common choice
• Cubic box is inefficient due to irrelevant water molecules in the corners.

Ideally you need a sufficiently large sphere of water surrounding the macromolecule, but that’s impossible because spheres can’t be packed to fill space.

• Ideal simulation system is a sphere of water surrounding the macromolecule, but spheres can’t be packed to fill space.

Octahedral and dodecahedral periodic boxes

A common alternatives that are closer to spherical are the dodecahedron (any polyhedron with 12 faces) or the truncated octahedron (14 faces). These shapes work reasonably well for globular macromolecules.

• The dodecahedron (12 faces) or the truncated octahedron (14 faces) are closer to sphere.

	Space filling with truncated octahedrons

• These shapes work reasonably well for globular macromolecules.

Triclinic periodic boxes

The triclinic box is the least symmetric of all types of periodic boxes. The triclinic system defines the unit cells by three basis vectors of unequal length, and the angles between these vectors must all be different from each other, and not 90 degrees.

In simulation packages, however, there usually are no such restrictions for triclinic boxes, which is why they are the most generic periodic boundary conditions. Any periodic box can be converted into a triclinic box with specific box vectors and angles.

• Any repeating shape that fills all of space has an equivalent triclinic unit cell.
• A periodic box of any shape can be represented by a triclinic box with specific box vectors and angles.

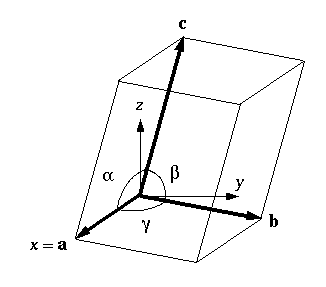
There are two reasons why triclinic boxes are useful: First, they can be used to simulate crystals that don’t have rectangular unit cells. In addition, the best triclinic cell has about 71% the volume of an ideal rectangular cell.

• The optimal triclinic cell has about 71% the volume of the optimal rectangular cell.

Box size

A good rule of thumb is to keep the box at least 10 Å away from the solute. Of course this assumes completely equilibrated system. If you are preparing a new system, make sure there is at least a margin of 13 Å between the solvent and the box, since the solvent will come closer to the solute during equilibration and the box will contract.

• The minimum box size should extend at least 10 nm from the solute.

In order to avoid short range interactions between a molecule and its images, the shortest periodic box vector should be at least twice as big as the cuf-off radius.

• The shortest periodic box vector should be at least twice bigger than the cuf-off radius.

The solvent molecules in simulations involving macromolecules should not “feel” both sides of a solute. In other words, there must be at least twice the cut-off distance between a macromolecule and any of its images.

• In simulations with macromolecules solvent molecules should not “feel” both sides of a solute.

When your simulation system is small make sure you do not set the cutoff too high!

Pitfalls

Solvated macromolecules rotate during simulations. Furthermore macromolecules may undergo conformational changes. Often these changes are of major interest and should not be restricted in any way.

Periodic boxes for elongated molecules are also elongated when the distance between the solute and the box is used to prepare them. If the smallest box dimension is not large enough rotation will result in the interaction between the molecule and its periodic images and lead to unphysically restricted dynamics. Thus, when setting up a periodic system, you must consider rotation of elongated macromolecules as well as possible changes in conformation.

Use of a cubical or dodecahedral box is one way to solve this problem. A disadvantage of such an approach is that you will need a lot of water to fill the box.

• A simulation system with elongated solute in cubic or dodecahedral box will have a large amount of water located far away from the solute.
• Consider using a narrow rectangular box.
• Rotation of elongated macromolecules and/or conformational changes must be taken in consideration.

Using a narrow box together with constraining rotational motion is more efficient [1]. Be aware, however, that the box shape itself may impact conformational dynamics by restricting motion in certain directions [2]. This effect may be significant when the amount of solvent is minimal.

• Constrain the rotational motion.
• The box shape itself may influence conformational dynamics by restricting motions in certain directions.

Specifying Periodic Box

GROMACS

The box specification is integrated into structure files. The box parameters can be set using the editconf program or manually. The editconf program accepts the following options:

-bt	Box type	triclinic, cubic, dodecahedron, octahedron
-box	Box vectors lengths, a, b, c	nm
-angles	Box vectors angles, bc, ac, ab	degrees
-d	Distance between the solute and the box	nm

Example:

module load StdEnv/2020 gcc gromacs
wget http://files.rcsb.org/view/1lyz.pdb
gmx pdb2gmx -f 1lyz.pdb -ff amber99sb-ildn -water spce -ignh
gmx editconf -f conf.gro -o conf_boxed.gro -d 1.0 -bt cubic

In the example above the editconf program will append box vectors to the structure file ‘conf.gro’ and save it in the file ‘conf_boxed.gro’. The 9 components of the three box vectors are saved in the last line of the structure file in the order: xx yy zz xy xz yx yz zx zy. Three of the values (xy, xz, and yz) are always zeros because they are duplicates of (yx, zx, and zy). The values of the box vectors components are related to the unit cell vectors \(a,b,c,\alpha,\beta,\gamma\) from the CRYST1 record of a PDB file with the equations:

\[xx=a, yy=b\cdot\sin(\gamma), zz=\frac{v}{(a*b*\sin(\gamma))}\] \[xy=0, xz=0, yx=b\cdot\cos(\gamma)\] \[yz=0, zx=c\cdot\cos(\beta), zy=\frac{c}{\sin(\gamma)}\cdot(cos(\alpha)-cos(\beta)\cdot\cos(\gamma))\] \[v=\sqrt{1-\cos^2(\alpha)-cos^2(\beta)-\cos^2(\gamma) +2.0\cdot\cos(\alpha)\cdot\cos(\beta)\cdot\cos(\gamma)}\cdot{a}\cdot{b}\cdot{c}\]

NAMD

Periodic box is specified in the run parameter file by three unit cell vectors, the units are Å.

# cubic box
cellBasisVector1 100 0 0
cellBasisVector2 0 100 0
cellBasisVector3 0 0 100

Alternatively periodic box parameters can be read from the .xsc (eXtended System Configuration) file by using the extendedSystem keyword. If this keyword is used cellBasisVectors are ignored. NAMD always generates .xsc files at runtime.

extendedSystem restart.xsc

Comparing periodic boxes

Using the structure file ‘conf.gro’ from the example above generate triclinic, cubic, dodecahedral and truncated octahedral boxes with the 15 Å distance between the solute and the box edge.

Which of the boxes will be the fastest to simulate?

References:

1. Molecular dynamics simulations with constrained roto-translational motions: Theoretical basis and statistical mechanical consistency
2. The effect of box shape on the dynamic properties of proteins simulated under periodic boundary conditions
3. Periodic box types in Gromacs manual

Key Points

• Periodic boundary conditions are used to approximate an infinitely large system.

• Periodic box should not restrict molecular motions in any way.

• The macromolecule shape, rotation and conformational changes should be taken into account in choosing the periodic box parameters.