Fast Methods to Evaluate Forces

Overview

Teaching: 30 min
Exercises: 0 min

Questions

• Why the computation of non-bonded interactions is the speed limiting factor?

• How are non-bonded interactions computed efficiently?

• What is a cutoff distance?

• How to choose the appropriate cutoff distance?

Objectives

• Understand how non-bonded interactions are truncated.

• Understand how a subset of particles for calculation of short-range non-bonded is selected.

• Learn how to choose the appropriate cutoff distance and truncation method.

• Learn how to select cutoff distance and truncation method in GROMACS and NAMD.

Challenges in calculation of non bonded interactions.

The most computationally demanding part of a molecular dynamics simulation is the calculation of the non-bonded terms of the potential energy function. Since the non-bonded energy terms between every pair of atoms must be evaluated, the number of calculations increases as the square of the number of atoms. In order to speed up the computation, only interactions between atoms separated by less than a preset cutoff distance are considered.

It is essential to use an efficient way of excluding pairs of atoms separated by a long distance in order to accelerate force computation. Such methods are known as “neighbour searching methods”.

• The number of non-bonded interactions increases as the square of the number of atoms.
• The most computationally demanding part of a molecular dynamics simulation is the calculation of the non-bonded interactions.
• Simulation can be significantly accelerated by limiting the number of evaluated non bonded interactions.
• Exclude pairs of atoms separated by long distance.
• Maintain a list of all particles within a predefined cutoff distance of each other.

Neighbour Searching Methods

The search for pairs of particles that are needed for calculation of the short-range non-bonded interactions is usually accelerated by maintaining a list of all particles within a predefined cutoff distance of each other.

Particle neighbours are determined either by dividing the simulation system into grid cells (cell lists) or by constructing a neighbour list for each particle (Verlet lists).

• Divide simulation system into grid cells - cell lists.
• Compile a list of neighbors for each particle by searching all pairs - Verlet lists.

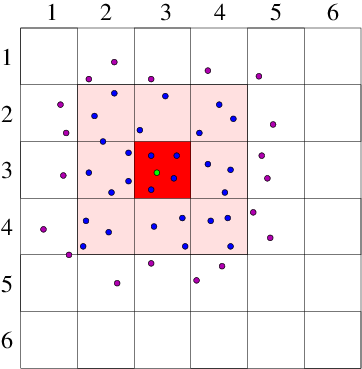
Cell Lists

The cell lists method divides the simulation domain into n cells with edge length greater or equal to the cutoff radius of the interaction to be computed. With this cell size, all particles within the cutoff will be considered. The interaction potential for each particle is then computed as the sum of the pairwise interactions between the current particle and all other particles in the same cell plus all particles in the neighbouring cells (26 cells for 3-dimensional simulation).

• Divide the simulation domain into cells with edge length greater or equal to the cutoff distance.
• Interaction potential of a particle is the sum of the pairwise interactions with all other particles in the same cell and all neighboring cells.

Verlet Lists

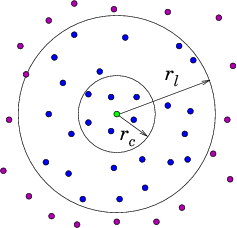
A Verlet list stores all particles within the cutoff distance of every particle plus some extra buffer distance. Although all pairwise distances must be evaluated to construct the Verlet list, it can be used for several consecutive time steps until any particle has moved more than half of the buffer distance. At this point, the list is invalidated and the new list must be constructed.

• Verlet list stores all particles within the cutoff distance plus some extra buffer distance.
• All pairwise distances must be evaluated.
• List is valid until any particle has moved more than half of the buffer distance.

Verlet offers more efficient computation of pairwise interactions at the expense of relatively large memory requirement which can be a limiting factor.
In practice, almost all simulations are run in parallel and use a combination of spatial decomposition and Verlet lists.

• Efficient computation of pairwise interactions.
• Relatively large memory requirement.
• In practice, almost all simulations use a combination of spatial decomposition and Verlet lists.

Problems with Truncation of Lennard-Jones Interactions and How to Avoid Them?

We have learned that the LJ potential is always truncated at the cutoff distance. A cutoff introduces a discontinuity in the potential energy at the cutoff value. As forces are computed by differentiating potential, a sharp difference in potential may result in nearly infinite forces at the cutoff distance (Figure 1A). There are several approaches to minimize the impact of the cutoff.

• LJ potential is always truncated at the cutoff distance.
• Truncation introduces a discontinuity in the potential energy.
• A sharp change in potential may result in nearly infinite forces.

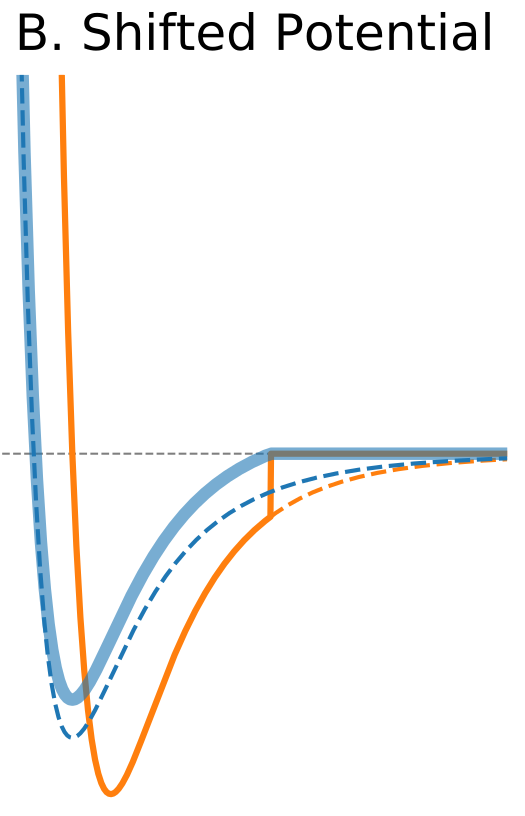
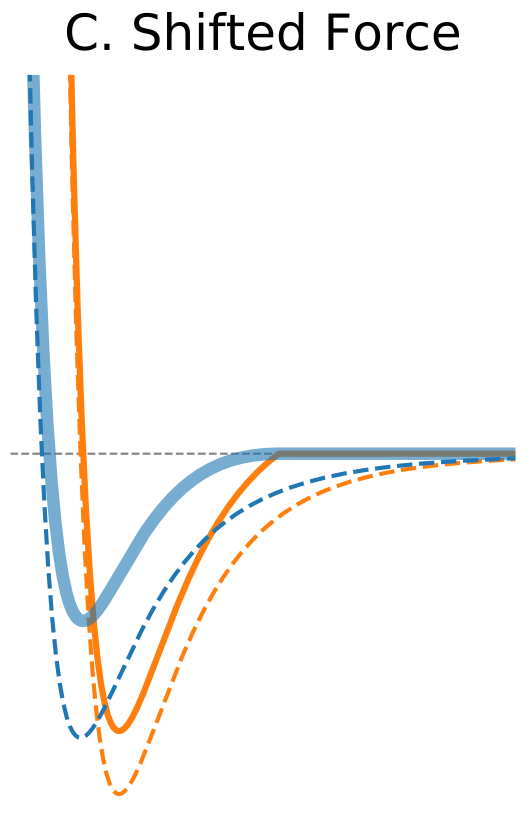
Figure 1. The Distance Dependence of Potential and Force for Different Truncation Methods

Shifted potential
The standard solution is to shift the whole potential uniformly by adding a constant at values below cutoff (shifted potential method, Figure 1B). This ensures continuity of the potential at the cutoff distance and avoids infinite forces. The addition of a constant term does not change forces at the distances below cutoff because it disappears when the potential is differentiated. However, it introduces a discontinuity in the force at the cutoff distance. Particles will experience sudden un-physical acceleration when other particles cross their respective cutoff distance. Another drawback is that when potential is shifted the total potential energy changes.</div>
Shifted Force
One way to address discontinuity in forces is to shift the whole force so that it vanishes at the cutoff distance (Figure 1C). As opposed to the potential shift method the shifted forces cutoff modifies equations of motion at all distances. Nevertheless, the shifted forces method has been found to yield better results at shorter cutoff values compared to the potential shift method (Toxvaerd, 2011).
Switching Function
Another solution is to modify the shape of the potential function near the cutoff boundary to truncate the non-bonded interaction smoothly at the cutoff distance. This can be achieved by the application of a switching function, for example, polynomial function of the distance. If the switching function is applied the switching parameter specifies the distance at which the switching function starts to modify the LJ potential to bring it to zero at the cutoff distance. The advantage is that the forces are modified only near the cutoff boundary and they approach zero smoothly.

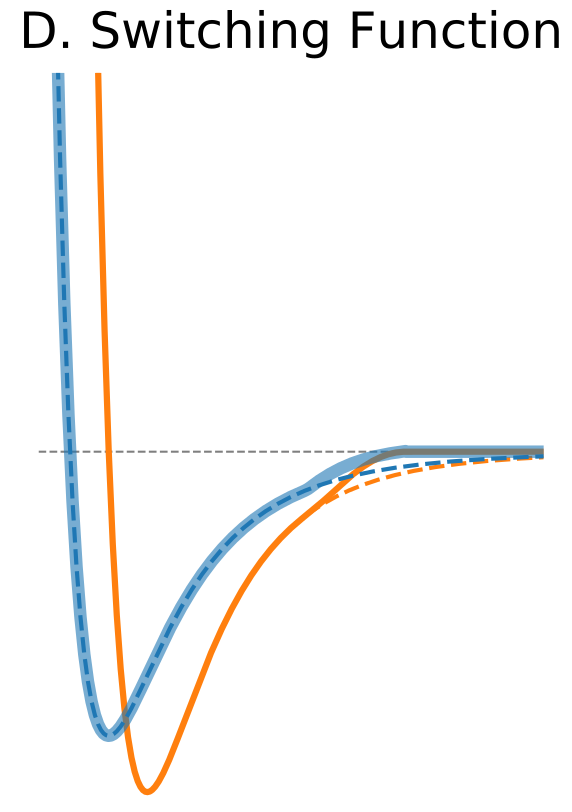Shifted potential
$\circ$ Shift the whole potential uniformly by adding a constant at values below cutoff. $\circ$ Avoids infinite forces. $\circ$ Does not change forces at the distances below cutoff. $\circ$ Introduces a discontinuity in the force at the cutoff distance. $\circ$ Modifies total potential energy.
Shifted Force
$\circ$ Shift the whole force so that it vanishes at the cutoff distance. $\circ$ Modifies equations of motion at all distances. $\circ$ Better results at shorter cutoff values compared to the potential shift.
Switching Function
$\circ$ Modify the shape of the potential function near cutoff. $\circ$ Forces are modified only near the cutoff boundary and they approach zero smoothly.

How to Choose the Appropriate Cutoff Distance?

A common practice is to truncate at 2.5 \(\sigma\) and this practice has become a minimum standard for truncation. At this distance, the LJ potential is about 1/60 of the well depth \(\epsilon\), and it is assumed that errors arising from this truncation are small enough. The dependence of the cutoff on \(\sigma\) means that the choice of the cutoff distance depends on the force field and atom types used in the simulation.

• A common practice is to truncate at 2.5 \(\sigma\).
• At this distance, the LJ potential is about 1/60 of the well depth \(\epsilon\).
• The choice of the cutoff distance depends on the force field and atom types.

For example for the O, N, C, S, and P atoms in the AMBER99 force field the values of \(\sigma\) are in the range 1.7-2.1, while for the Cs ions \(\sigma=3.4\). Thus the minimum acceptable cutoff, in this case, is 8.5.

In practice, increasing cutoff does not necessarily improve accuracy. There are documented cases showing opposite tendency (Yonetani, 2006). Each force field has been developed using a certain cutoff value, and effects of the truncation were compensated by adjustment of some other parameters. If you use cutoff 14 for the force field developed with the cutoff 9, then you cannot claim that you used this original forcefield. To ensure consistency and reproducibility of simulations, you should choose a cutoff that is appropriate for the force field.

• Increasing cutoff does not necessarily improve accuracy.
• Each force field has been developed using a certain cutoff value, and effects of the truncation were compensated by adjustment of some other parameters.
• To ensure consistency and reproducibility of simulation you should choose the cutoff appropriate for the force field:

Table 1. Cutoffs Used in Development of the Common Force Fields

Properties that are very sensitive to the choice of cutoff

Different molecular properties are affected differently by various cutoff approximations. Examples of properties that are very sensitive to the choice of cutoff include the surface tension (Ahmed, 2010), the solid–liquid coexistence line (Grosfils, 2009), the lipid bi-layer properties (Huang, 2014), and the structural properties of proteins (Piana, 2012).

• the surface tension (Ahmed, 2010),
• the solid–liquid coexistence line (Grosfils, 2009),
• the lipid bi-layer properties (Huang, 2014),
• the structural properties of proteins (Piana, 2012).

For such quantities even a cutoff at 2.5 \(\sigma\) gives inaccurate results, and in some cases the cutoff must be larger than 6 \(\sigma\) was required for reliable simulations (Grosfils, 2009).

Effect of cutoff on energy conservation

Cutoff problems are especially pronounced when energy conservation is required. The net effect could be an increase in the temperature of the system over time. The best practice is to carry out trial simulations of the system under study without temperature control to test it for energy leaks or sources before a production run.

• Short cutoff may lead to an increase in the temperature of the system over time.
• The best practice is to carry out trial simulations without temperature control to test it for energy leaks or sources before a production run.

Truncation of the Electrostatic Interactions

Electrostatic interactions occurring over long distances are known to be important for biological molecules. Electrostatic interactions decay slowly and simple increase of the cutoff distance to account for long-range interactions can dramatically raise the computational cost. In periodic simulation systems, the most commonly used method for calculation of long-range electrostatic interactions is particle-mesh Ewald. In this method, the electrostatic interaction is divided into two parts: a short-range contribution, and a long-range contribution. The short-range contribution is calculated by exact summation of all pairwise interactions of atoms separated by a distance that is less than cutoff in real space. The forces beyond the cutoff radius are approximated on the grid in Fourier space commonly by the Particle-Mesh Ewald (PME) method.

• The electrostatic interaction is divided into two parts: a short-range and a long-range.
• The short-range contribution is calculated by exact summation.
• The forces beyond the cutoff radius are approximated using Particle-Mesh Ewald (PME) method.

Selecting Neighbour Searching Methods

GROMACS

Neighbour searching is specified in the run parameter file mdp.

cutoff-scheme  =  group
; Generate a pair list for groups of atoms. Since version 5.1 group list has been deprecated and only Verlet scheme is available.

cutoff-scheme  =  Verlet
; Generate a pair list with buffering. The buffer size is automatically set based on verlet-buffer-tolerance, unless this is set to -1, in which case rlist will is used.

; Neighbour search method.
ns-type = grid
; Make a grid in the box and only check atoms in neighboring grid cells.

ns-type = simple
; Loop over every atom in the box.

nstlist = 5
; Frequency to update the neighbour list. If set to 0 the neighbour list is constructed only once and never updated. The default value is 10.

NAMD

When run in parallel NAMD uses a combination of spatial decomposition into grid cells (patches) and Verlet lists with extended cutoff distance.

stepspercycle 10
# Number of timesteps in each cycle. Each cycle represents the number of timesteps between atom reassignments. Default value is 20.

pairlistsPerCycle 2
# How many times per cycle to regenerate pairlists. Default value is 2.

Selecting LJ Potential Truncation Method

GROMACS

Truncation of LJ potential is specified in the run parameter file mdp.

vdw-modifier = potential-shift
;  Shifts the VDW potential by a constant such that it is zero at the rvdw.

vdw-modifier = force-switch
;  Smoothly switches the forces to zero between rvdw-switch and rvdw.

vdw-modifier = potential-switch
;  Smoothly switches the potential to zero between rvdw-switch and rvdw.

vdw-modifier = none

rvdw-switch = 1.0
;  Where to start switching.

rvdw = 1.2
;  Cut-off distance

NAMD

Truncation of LJ potential is specified in the run parameter file mdin.

cutoff 12.0
# Cut-off distance common to both electrostatic and van der Waals calculations

switching on
# Turn switching on/off. The default value is off.

switchdist 10.0
# Where to start switching

vdwForceSwitching on
# Use force switching for VDW. The default value is off.

AMBER force fields

AMBER force fields are developed with hard truncation. Do not use switching or shifting with these force fields.

Selecting Cutoff Distance

GROMACS

Cutoff and neighbour searching is specified in the run parameter file mdp.

rlist = 1.0
; Cutoff distance for the short-range neighbour list. Active when verlet-buffer-tolerance = -1, otherwise ignored.

verlet-buffer-tolerance = 0.002
; The maximum allowed error for pair interactions per particle caused by the Verlet buffer. To achieve the predefined tolerance the cutoff distance rlist is adjusted indirectly. To override this feature set the value to -1. The default value is 0.005 kJ/(mol ps).

NAMD

When run in parallel NAMD uses a combination of spatial decomposition into grid cells (patches) and Verlet lists with extended cutoff distance.

pairlistdist 14.0
# Distance between pairs for inclusion in pair lists. Should be bigger or equal than the cutoff. The default value is cutoff.

cutoff 12.0
# Local interaction distance. Same for both electrostatic and VDW interactions.

Key Points

• The calculation of non-bonded forces is the most computationally demanding part of a molecular dynamics simulation.

• Non-bonded interactions are truncated to speed up simulations.

• The cutoff distance should be appropriate for the force field and the size of the periodic box.