Degrees of Freedom

Overview

Teaching: 10 min
Exercises: 0 min

Questions

• How is kinetic energy contained and distributed in a dynamic molecular system

• Why constraints are used in MD simulations, and how they can affect dynamics

Objectives

Molecular degrees of freedom

Molecular degrees of freedom refer to the number of unique ways a molecule may move (increase its kinetic energy). Thus the molecular degrees of freedom describe how kinetic energy is contained and distributed in a molecule. Dynamical molecular systems are characterized by numerous degrees of freedom. The motion of molecules can be decomposed into translational, rotational, and vibrational components.

• The number of unique ways a molecule may move (increase its kinetic energy).
• Describe how kinetic energy is contained and distributed in a molecule.
• Translational, rotational, and vibrational components.

Equipartition theorem

On average, when thermal energy is added to a system, the energy is shared equally among the degrees of freedom (equipartition theorem). In other words, classical equipartition principle states that every (quadratic) degree of freedom contributes equally to the total energy in thermal equilibrium. Each degree of freedom has an average energy of \(\frac{1}{2}k_BT\) and contributes \(\frac{1}{2}k_B\) to the system’s heat capacity.

• The energy is shared equally among the degrees of freedom (equipartition theorem).
• Each degree of freedom has an average energy of \(\frac{1}{2}k_BT\) and contributes \(\frac{1}{2}k_B\) to the system’s heat capacity.

Degrees of freedom and thermodynamics properties

When the same amount of kinetic energy flows into simulation systems containing different types of molecules, their temperature will change by a different amount. The more places (degrees of freedom) there are to put the energy the less the temperature change will be.

The number of degrees of freedom is an important quantity allowing us to estimate various thermodynamic variables for a simulation system (for example heat capacity, entropy, temperature).

• When kinetic energy is applied to simulation systems containing molecules with different degrees of freedom, the temperature increase will vary.
• If energy is spread over many places (degrees of freedom), the temperature will change less.
• The number of degrees of freedom is an essential quantity for estimating various thermodynamic variables for a simulation system (such as heat capacity, entropy, and temperature).

Translational degrees of freedom

An atom or a molecule can move in three dimensions. Thus, any atom or molecule has three degrees of freedom associated with translational motion of the center of mass with respect to the X, Y, and Z axes.

• The three translational degrees of freedom in three dimensions provide \(\frac{3}{2}k_BT\) of energy.

• Atoms and molecules have three degrees of freedom associated with the translation of their centers of mass about each coordinate axis.
• Translational degrees of freedom in three dimensions yield \(\frac{3}{2}k_BT\) of energy.

Rotational degrees of freedom

From the classical point of view atoms have a negligible amount of rotational energy because their mass is concentrated in the nucleus. Since radius of a nucleus is about \(10^{-15}\) m, atoms have negligible rotational moment of inertia. (From the QM point of view rotation of an atom has no meaning because such rotations lead to configurations which are indistinguishable from the original configuration). But molecules are different in this respect, they can have rotational kinetic energy. A linear molecule, has two rotational degrees of freedom, because it can rotate about either of two axes perpendicular to the molecular axis. The rotations along the molecular axis have a negligible amount of rotational energy because the mass is concentrated very close to the axis of rotation. A nonlinear molecule, where the atoms do not lie along a single axis, like water, has three rotational degrees of freedom, because it can rotate around any of three perpendicular axes.

• The rotational degrees of freedom contribute \(k_BT\) to the energy of linear molecules and \(\frac{3}{2}k_BT\) to the energy of non-linear molecules.

• Atoms have a negligible amount of rotational energy because their mass is concentrated in the nucleus which is very small (about \(10^{-15}\) m).
• A linear molecule, has two rotational degrees of freedom.
• A nonlinear molecule, where the atoms do not lie along a single axis, has three rotational degrees of freedom, because it can rotate around any of three perpendicular axes.
• The rotational degrees of freedom contribute \(k_BT\) to the energy of linear molecules and \(\frac{3}{2}k_BT\) to the energy of non-linear molecules.

Vibrational degrees of freedom

A molecule can also vibrate. A diatomic molecule has one molecular vibration mode, where the two atoms oscillate back and forth with the chemical bond between them acting as a spring.

A molecule with N atoms has more complicated modes of molecular vibration, with 3N − 5 vibrational modes for a linear molecule and 3N − 6 modes for a nonlinear molecule.

• A diatomic molecule has one molecular vibration mode.
• A linear molecule with N atoms has 3N − 5 vibrational modes.
• A non-linear molecule with N atoms has 3N − 6 vibrational modes.

Angle bend	Symmetric stretch	Asymmetric stretch

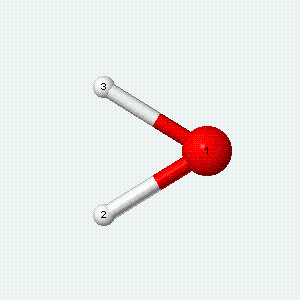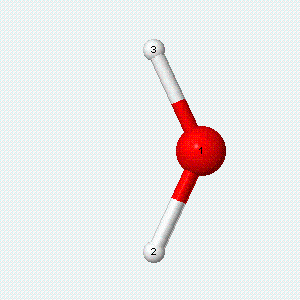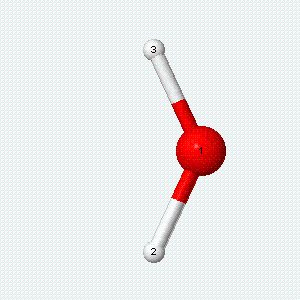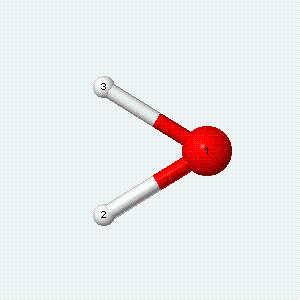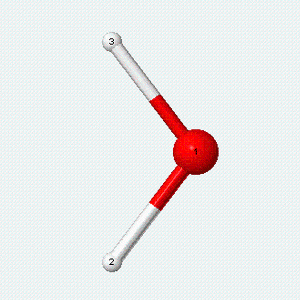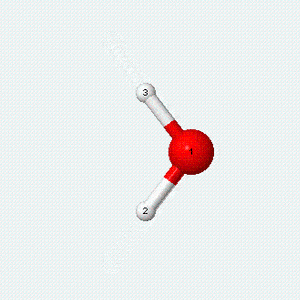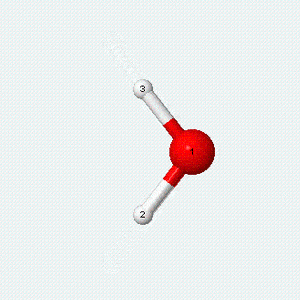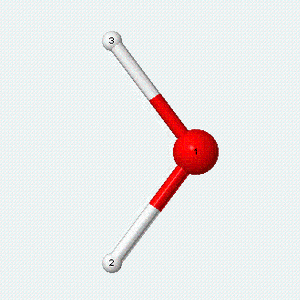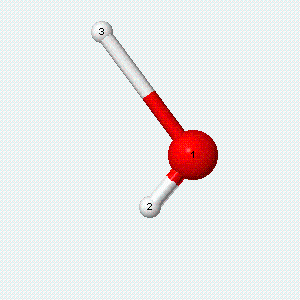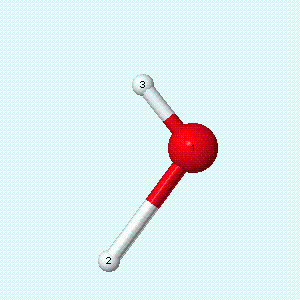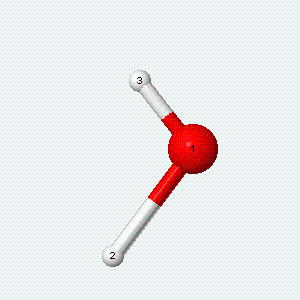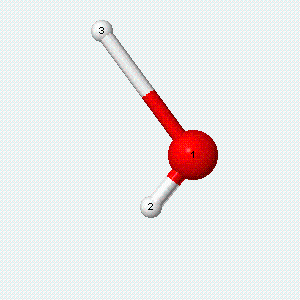Each vibrational mode has two degrees of freedom for energy. The kinetic energy of moving atoms is one degree of freedom, and the potential energy of spring-like chemical bonds is another.

Each vibrational degree of freedom provides \(k_BT\) of energy. However, this is valid only when \(k_BT\) is much bigger than spacing between vibrational states. At low temperature this condition is not satisfied, only a few vibrational states are occupied and the equipartition principle is not typically applicable.

• There are two degrees of freedom for each vibrational mode.
• One degree involves the kinetic energy of the moving atoms, and the other involves the potential energy of the springlike chemical bond(s).
• Each vibrational degree of freedom contributes \(k_BT\) to the energy of a molecule. However, this is valid only when \(k_BT\) is much bigger than energy spacing between vibrational modes.
• At low temperature this condition is not satisfied, only a few vibrational states are occupied and the equipartition principle is not typically applicable.

Increasing efficiency of thermodynamic sampling.

To compute thermodynamic quantities with a molecular simulation, we sample a configuration space with the dimensionality determined by the number of degrees of freedom. Thus, by reducing the number of degrees of freedom (of course when physically justifiable) we can increase thermodynamic sampling efficiency.

By reducing the number of degrees of freedom we can increase thermodynamic sampling efficiency.

Constraints are used in most molecular dynamics simulations, since the maximum length of the time step for integrating the equations of motion is limited by the frequency of the fastest motions in the system. Bond constraints that remove the rapid vibrational modes eliminate those degrees of freedom and make possible to use longer time steps without losing conservation of energy. Constraints including angles and dihedrals can be also applied.

• Force fields remove the electrons’ degrees of freedom by replacing them with atom centered charges.
• An implicit solvent model eliminates the degrees of freedom associated with the solvent molecules.
• Bond constraints eliminate vibrational degrees of freedom and make possible to use longer time steps.
• Constraints including angles and dihedrals can be also applied.

Reduction of the number of degrees of freedom may lead to artifacts.

Applying constraints, however, can affect the simulation by restricting the motions associated with the specified degrees of freedom. For example it was found that bond and angle constraints slow down dihedral angle transitions (Toxvaerd, 1987), shift the frequencies of the normal modes in biomolecules (Tobias and Brooks, 1988), and perturb the dynamics of polypeptides (Hinsen and Kneller, 1995).

Bond and angle constraints can:

• slow down dihedral angle transitions [1]
• shift the frequencies of the normal modes in biomolecules [2]
• perturb the dynamics of polypeptides [3].

Key Points

• Degrees of Freedom in Rigid bodies.

• Constraints decrease the number of degrees of freedom

• Imposing constraints can affect simulation outcome